Join us at the International Thermal Conductivity Conference (ITCC) and the International Thermal Expansion Symposium (ITES).
February 16, 2024
May 4, 2021
September 26, 2019
May 25, 2021
October 30, 2019
November 30, 2017
Note: This is a blog post describing the use of the Rule of Mixtures Calculator.
If you are looking to use the calculator, click the button below.
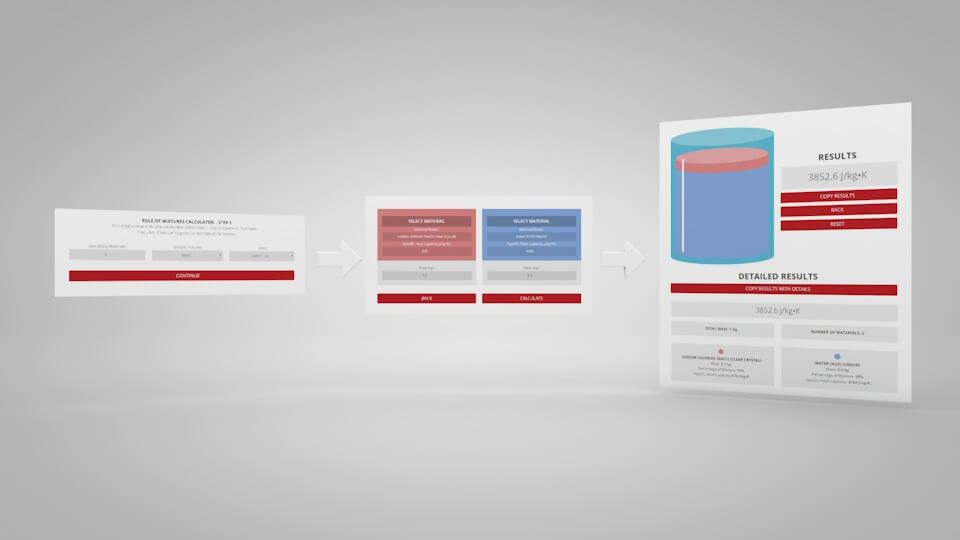
The Rule of Mixtures Calculator, newly released by Thermtest Inc., is an invaluable tool for estimating the specific heat capacity of mixtures containing any number of materials. Using the mass and specific heat capacity of each component, the Rule of Mixtures Calculator calculates the specific heat capacity of the entire sample. In addition to the Rule of Mixtures Calculator, a materials database that includes the specific heat capacities of 1000+ materials can be found on the Thermtest website. The following post delves into the theory behind The Rule of Mixtures Calculator, how to use it, and present real-world examples to demonstrate its usefulness.
Table of Contents

The mass of each individual component is equivalent to the total mass of the mixture, which can theoretically be broken down into separate parts.
As previously stated, the calculator uses the rule of mixtures formula to estimate the specific heat capacity of a solution with multiple components. Firstly, what is specific heat capacity, and why is a specific heat capacity calculator useful for mixtures? To answer these questions, let’s analyze the units of specific heat capacity.
\[ \left(C_{p}\right) = \frac{J}{{kg}\cdot^{\circ}\mathrm{C}}\]
In the previous equation, \(J\) represents energy in joules, \(kg\) is a unit of mass in kilograms, and \(^{\circ}\mathrm{C}\) is a unit of temperature in degrees Celsius. Therefore, specific heat capacity is the amount of energy needed to raise one kilogram of material, one degree. In other words, the specific heat capacity represents a material’s ability to store energy. Next, how can we use the rule of mixtures to calculate specific heat?
Correspondingly, the first step to determining the specific heat capacity of a mixture is to link each component in the mixture through the first law of thermodynamics. Markedly, the first law of thermodynamics states that energy cannot be created, or destroyed. Notably, this principle can be related to the following energy balance equation, where ‘Q’ refers to the total energy of a mixture in units of joules.
\[Q_{mixture}=Q_{1}+Q_{2}\]
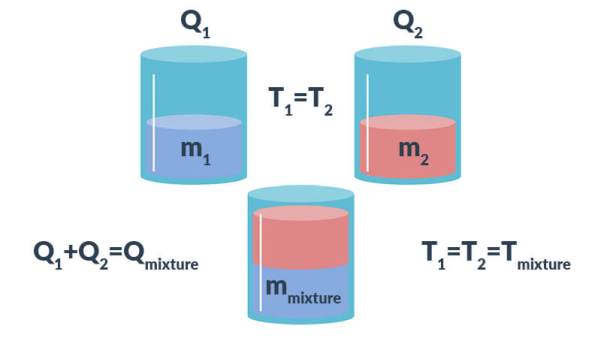
Figure 1. A simple representation of the energy balance equation applied to mixtures.
Where ‘\(Q\)’ is equal to:
\[{Q}={m}\cdot{C}_{p}\cdot\Delta{T}\]
Next, to calculate the total energy of the mixture (\(Q\)), the specific heat capacity (\(C_{p}\)) must be multiplied by the actual mass (\(m\)) and temperature difference (\(\Delta{T}\)) of each material within the solution. The total energy of the mixture is a product of these materials, assuming energy is not lost, or gained, during the mixing process. Moreover, it is presumed that the change in temperature is uniform. So, ‘\(\Delta{T}\)’ can be eliminated from the following equation, which is a combination of the previous two energy equations.
\[m_{mixture}\cdot{C}_{{p}\,mixture}\cdot\Delta{T} =\cdots\]
Finally, the rule of mixtures for specific heat capacity can be derived through some rearranging to provide the final equation:
\[C_{p\,mixture}=\Big(\frac{m_{1}}{m_{mixture}}\Big)C_{p\,1}+\Big(\frac{m_{2}}{m_{mixture}}\Big)C_{p\,2}\]
This equation can be adjusted to approximate the specific heat capacity of a mixture with an infinite number of components when the mass and specific heat capacity of each material is known, as well as the mass of the mixture. As each new material is added to the energy balance equation, the resultant equation is:
\[C_{p\,mixture}=\Big(\frac{m_{1}}{m_{mixture}}\Big)C_{p\,1}+\Big(\frac{m_{2}}{m_{mixture}}\Big)C_{p\,2}+\Big(\frac{m_{3}}{m_{mixture}}\Big)C_{p\,3}+\Big(\frac{m_{4}}{m_{mixture}}\Big)C_{p\,4} \]
The Rule of Mixtures Calculator uses the above equation to approximate the specific heat capacity of a mixture. Furthermore, the mass of each material can be substituted with volume.
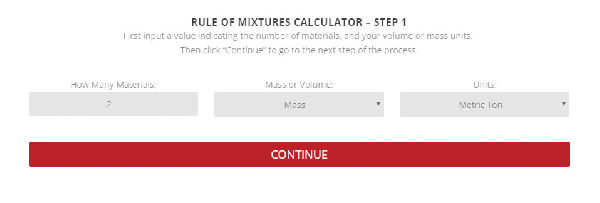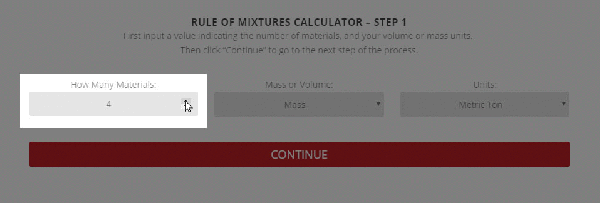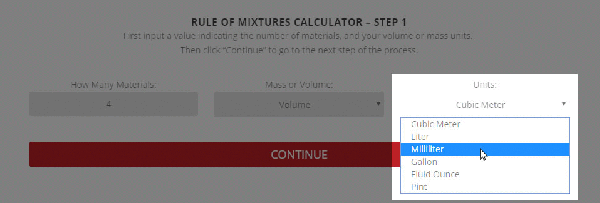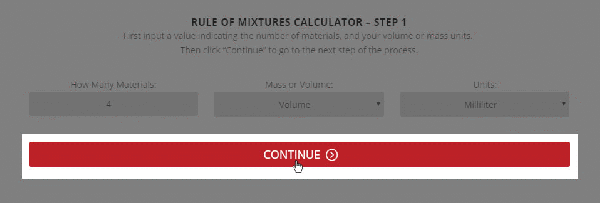
Step 1 – The initial setup for calculating specific heat capacity of a mixture.
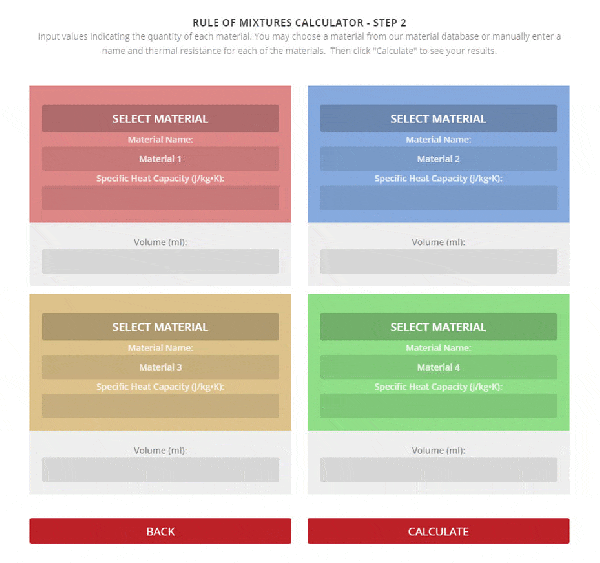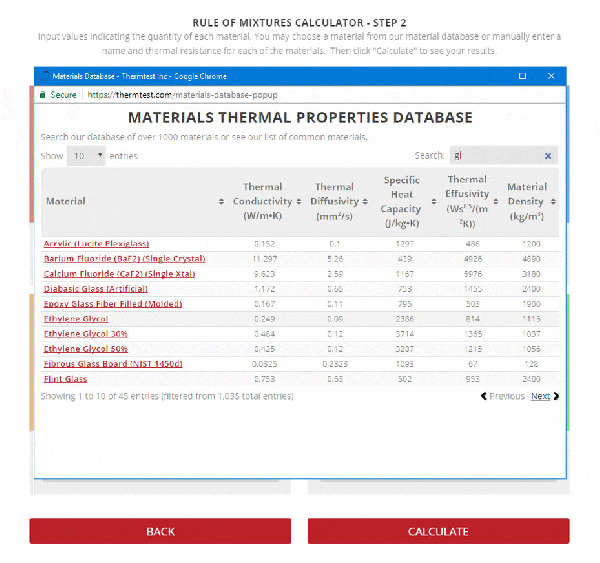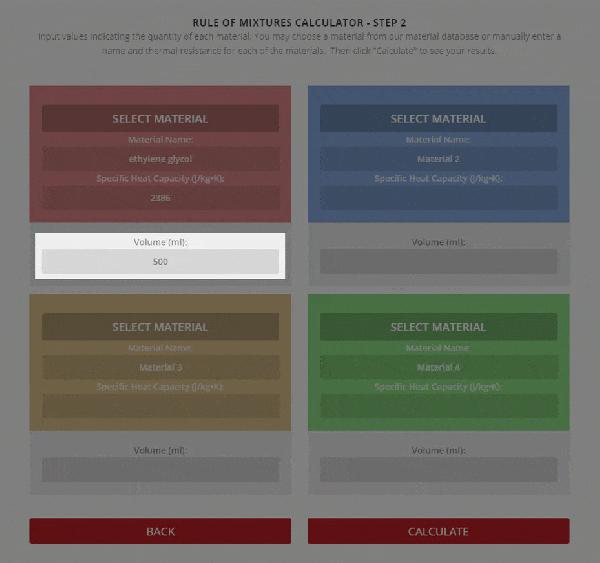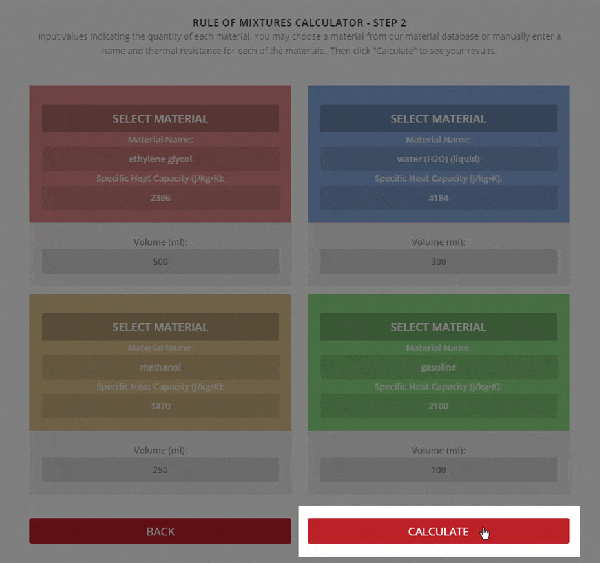
Step 2 – Enter the name, thermal resistance, and the mass or volume of each material.
To use the calculator, first select the number of components in the mixture. Then, input their respective masses, or volume, and their specific heat capacities. Once this is complete, the calculator will produce a specific heat capacity estimation. Correspondingly, the specific heat capacities used for the calculation can be selected from Thermtest’s materials database, as mentioned previously. In addition to specific heat capacity, the materials database also includes thermal conductivity, thermal diffusivity, thermal effusivity and material density values. The following examples demonstrate applications where the Rule of Mixtures Calculator would be useful.
A common myth most people believe to be true, is the act of adding salt to water, in hopes of shortening the mixture’s boiling time. The Rule of Mixtures Calculator can be used to demonstrate how the addition of salt would affect the specific heat capacity, and therefore boiling point of the solution. As mentioned previously, specific heat capacity determines how quickly a material will rise in temperature. For the purpose of this example, imagine that 0.1 kg of NaCl is being added to 0.9 kg of water. As these values are inputted into the calculator, an estimation of the specific heat capacity of the solution will be generated.
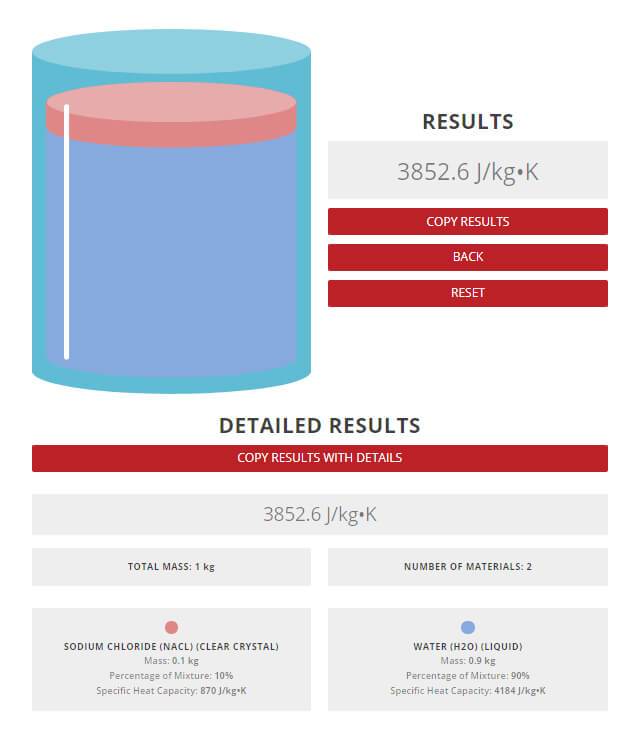
Results from the Rule of Mixtures Calculator.
The results of the calculation indicate that the specific heat capacity of the saline mixture would be approximately 3853 J/kg°C. In comparison, literature values report a specific heat capacity of 3700 J/kg °C, for for such a mixture. Moreover, the calculator estimated the specific heat capacity within 4% of the actual value, demonstrating its reliability and accuracy.
The next property to investigate is the boiling point of water; expected to decrease after the addition of salt. However, as seen in Figure 2, the salt will naturally increase the boiling point of the solution, and subsequently slow down the boiling time of the salt and water solution.
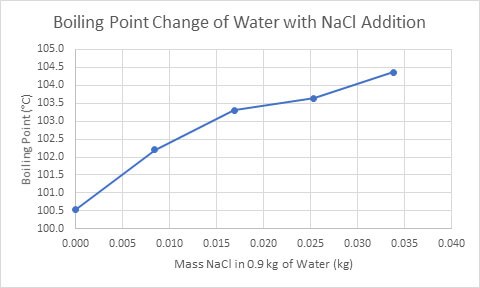
Figure 2. The change in boiling point of a salt and water solution as the mass of NaCl increases (Mas, 2016).
Antifreeze (ethylene glycol) is the most common commercial coolant used in vehicles. Antifreeze lowers the freezing point of fluids to prevent them from freezing in sub-zero temperatures (Figure 3). Despite it’s relatively high freezing point, water is typically added to antifreeze.
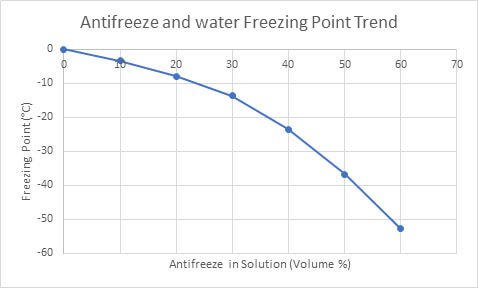
Figure 3. The freezing point of water as antifreeze volumes increase (Ethylene Glycol Heat-Transfer Fluid, 2017).
According to literature values, the specific heat capacity of water is 4184 J/kg°C, double the specific heat capacity of antifreeze. For this reason, water is able to store twice as much energy as antifreeze, allowing energy to be carried away from the engine faster than pure antifreeze.
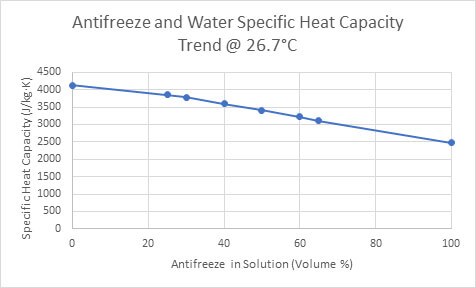
Figure 4. The specific heat capacity of an antifreeze-water solution as the volume of antifreeze increases (Ethylene Glycol Heat-Transfer Fluid, 2017).
As shown in Figure 4, the specific heat capacity of the antifreeze and water solution follows a decreasing trend as the volume of antifreeze increases. Consequently, mixing the two liquids merges the low freezing point of antifreeze, with the high specific heat capacity of water. With this in mind, the Rule of Mixtures Calculator can be applied to this scenario to determine the perfect antifreeze to water ratio to optimize the specific heat capacity of the solution. In the next example, the calculator can be used to prevent deformations in asphalt.
How can understanding energy storage help to reduce deformations in asphalt? Deformations occur when temperature changes cause asphalt to expand and contract. Accordingly, this problem can be solved by improving the specific heat capacity of asphalt, allowing the temperature of the asphalt to remain consistent, as more energy would be required to alter it.
In an article by Chen et al. (2012), phase change materials (PCMs) were used to improve asphalt’s energy storage ability. PCMs store energy in the form of sensible heat and latent heat. Latent heat stores most energy in the form of a phase change, whereas sensible heat stores energy through a temperature change. As a result, this energy is therefore influenced by specific heat capacity. During this study, it was found that sensible heat energy storage increased, when PCMs were mixed with asphalt. When the PCM/asphalt composite was combined with large amounts of energy storage from latent heat, the asphalt remained at a more constant temperature. At this constant temperature, cracks and deformations would be reduced.
| Mixture Type | Thermal Conductivity | Thermal Diffusivity | Volumetric Heat Capacity |
|---|---|---|---|
| (Units) | (W/m∙K) | (mm2/s) | (MJ/m3∙K) |
| Control Samples | 1.459 | 0.603 | 2.420 |
| Samples with PCM-L | 1.543 | 0.690 | 2.236 |
| Samples with PCM-Z | 1.371 | 0.553 | 2.478 |
The Rule of Mixtures Calculator can be used to estimate the amount of PCMs to combine with asphalt to achieve the desired specific heat capacity. For more information regarding the thermal conductivity of this example, TPS was used to conduct measurements on asphalt, and the results can be viewed in an application page.
Up to this point, only mixtures with two components have been discussed. Similarly, the next example demonstrates how the Rule of Mixtures Calculator can be applied to mixtures containing more than two materials.
Although concrete is a strong and affordable construction material, like asphalt, it is susceptible to cracking when temperature gradients form. Once exposed to heat, the concrete will expand. Once exposed to cooler temperatures, concrete will contract. Provided this change occurs rapidly, cracks will form in the concrete. Additionally, the formation of temperature gradients induces stress on the location where the two temperatures meet, which also causes cracks and deformations.
In a study conducted by Xu and Chung (2000), concrete with high specific heat capacity and thermal conductivity was produced by adding silane and silica fume (Figure 5).
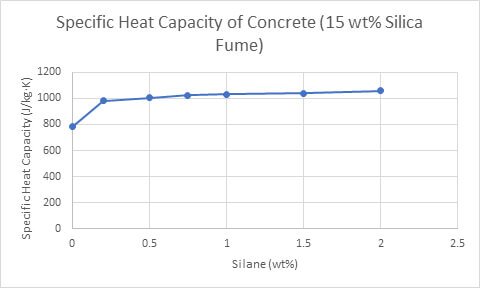
Figure 5. The effect of increasing silane concentrations (15 wt% silica fume) on the specific heat capacity of concrete (Yunsheng Xu, 2000).
Temperature gradients are less likely to form in concretes with high specific heat capacities, as they store more energy per degree. As a result, these concretes are able to quickly compensate for temperature gradients, as energy travels through them at a higher rate. The Rule of Mixtures calculator will help estimate the amount of silane, silica fume, cement paste and water needed to produce a concrete sample with an ideal specific heat capacity.
The Rule of Mixtures Calculator can approximate the specific heat capacity of a mixture with any number of units, with the input of known masses and specific heat capacities. Additionally, specific heat capacities can be selected from Thermtest’s very own materials database, which includes the thermal properties of more than 1000 different materials. The Rule of Mixtures Calculator is useful for a variety of applications. Whether it’s to find the perfect ratio of antifreeze to water, to approximate a value for comparison, or just to play around with, the Rule of Mixtures Calculator quickly and efficiently estimates the specific heat capacity of mixtures.