
October 30, 2019
Thermal expansion is the phenomenon where an object or body expands in reaction to being heated. Thermal expansion is most obvious in gasses and liquids but can still have a substantial effect on solids.

Figure1: railroad tracks bent due to linear thermal expansion
The thermal properties of a solid are a very important aspect in the design of factories and products. If thermal expansion is not considered during construction and design the result could be major structural damage in a machine or building. Countless measures have been taken to prevent this and many ingenious technologies are developed relying on this phenomenon. The amount that a material expands can be explained by considering a coefficient corresponding to the fractional growth of the material per degree change in temperature. This coefficient is called the coefficient of thermal expansion and is used to predict the growth of materials in response to a known temperature change. The larger this coefficient is for a material, the more it will expand per degree temperature increase.
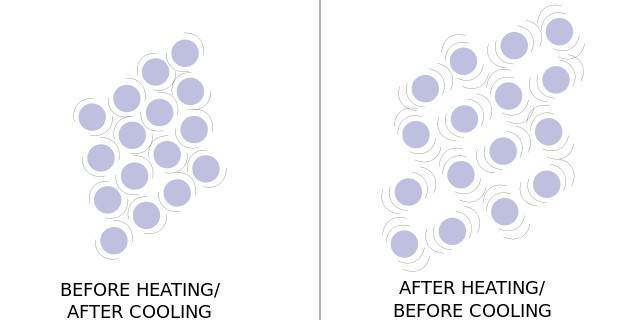
Figure 2: diagram of atomic vibrations before and after heating.
When a body is heated, it is accepting and storing energy in its atoms in the form of kinetic energy. This expose to an increased temperature causes an atom’s natural vibrations to grow stronger and more pronounced. This increase in vibration pushes against the inter-molecular forces, allowing the atoms or molecules to become farther apart and the body to grow larger. The amount by which a substance expands in reaction to a change in temperature is mathematically represented by a coefficient of thermal expansion. This coefficient is unique to each material and is based on their other physical properties. The higher a coefficient of thermal expansion a material has, the more it will expand in reaction to being heated.
Crystals tend to have the lowest thermal expansion coefficients because their structure is extremely uniform and structurally sound. Diamond has the lowest known thermal expansion coefficient of all naturally occurring materials. The solids with the highest coefficients of thermal expansion are the ones that have weak inter-molecular bonds, typically polymers, which also tend to have low melting points. The reason for this is that weaker bonds are overcome with less vibrational energy. Metals tend to have relatively low coefficients, but they also have very high melting points, and they are not as perceptible to a material failure caused by the stress of expansion. This makes metals ideal candidates to use when measuring thermal expansion.
Measurements of a change in volume caused by a physical or chemical process is called dilatometry. An instrument designed to measure the change in volume of some substance is called a dilatometer. The most common example of a dilatometer is a mercury thermometer, which measures the volume and the change in volume of the trapped mercury which is used to determine the temperature of the surrounding environment. Dilatometers can also be used to calculate the coefficient of thermal expansion. To determine the coefficient, the volume of the material is carefully measured as the temperature rises from one known value to another.
There are a few examples of dilatometers that are designed to measure the volume of solid metal pieces to determine thermal expansion. One design is the capacitance dilatometers. In this design, one plate of a capacitor is movable, and the sample is placed behind it, so when it expands it pushes the movable plate closer to the other plate. A more modern and accurate example would be the laser dilatometer, which constantly measures the dimensions of the sample with lasers. One of the most versatile designs is the optical dilatometer which is simply a digital camera using an optical group to measure the variations in the sample’s size.
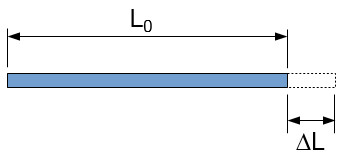
Figure 3: diagram showing the effect of linear thermal expansion.
Gases and liquids always expand volumetrically, expanding within the confines of their containers. In theory, solids always expand volumetrically as well but because they hold their shape it makes them appear to expand differently. For example, when a long metal rod is heated its atoms travel farther apart in all three dimensions. During this expansion, the rods cross-sectional growth will hardly be noticeable compared to its growth lengthwise. Since the rod is initially very thin there is a relatively small number of atoms pushing against each other in the cross-sectional direction. In the lengthwise direction however, there is a larger number of atoms lined up, and when they all push against each other it forms a chain reaction that pushes the total length of the rod to be much larger than it was.
Objects with dimensions like this can be regarded as only expanding in the one dimension. They are thought to have a coefficient of linear thermal expansion instead of a coefficient of volume thermal expansion. This coefficient acts the same as the three-dimensional coefficient of expansion, except it corresponds to the fractional increase in length (instead of volume) per degree temperature. The same is true about coefficients of area expansion in two dimensions for flat plates. From this observation it can be determined that the amount that a body expands in response to a rise in temperature is linearly dependent on the original size of the body.
An observational approach can be adopted to find a useful equation to predict the resulting size of a body after a temperature change. As explained above, the amount that a linear substance expands is linearly related to the original length, (L0). Observation shows that the expansion is also approximately linearly related to the change in temperature (dT). It is also obvious through observation that all materials expand differently. Due to this variation in expansion patterns, it can be determined that other physical aspects influence thermal expansion. A coefficient is used to account for a substance’s additional physical properties. This coefficient is known as the coefficient of linear thermal expansion, (α). The equation for the final length would therefore be
L = L0 + L0*α*dT
Which can be re arranged for α
α = (L – L0)/(L0*dT)
Or if it is said that the change in length, L – L0, is dL
α = 1/L0 * dL/dT
The same logic can be used to build the equations regarding volume expansion. They are similar except the length variable would be exchanged for volume and the linear expansion coefficient would be changed to volumetric. To ensure accuracy, it is ideal to derive the volume expansion equation from the linear equation.
V = L3 = [ L0 + L0*α*dT ]3
From analysis using the linear method, it is apparent that the value of α is usually in the parts per million range (x10-6). Since the value is so small, both the terms that raise it to a power above one result in such a small value that they will have almost no effect on the result. These terms can be ignored by approximating slightly.
V = L03[ 1 + 3α*dT]
= V0[ 1 + 3α*dT]
Since α is a constant unknown coefficient, it can be said that 3α is a new constant unknown coefficient named the coefficient of volume thermal expansion, (β).
V = V0 + V0*β*dT
β = 1/V0 * dV/dT
This form of the equation could now be used to find the coefficients of thermal expansion of materials after measuring them with a dilatometer over a known temperature change. These equations display that both the linear and volume expansion coefficients have units of Kelvin-1, Celcius-1, or Fahrenheit-1.
With a dilatometer and a thermometer, it is very straight forward to conduct an experiment on a sample and then follow the equation to calculate the thermal expansion coefficients. Aluminum is a convenient material to study with this method, as it has a very high expansion coefficient for a metal. Stainless steels are perhaps the most commonly measured due to their abundant use in many applications.
These steels have a coefficient that is about average for metals, however, they are not extremely valuable like silver and gold. A lack of thermal knowledge during engineering and design can result in the collapse of bridges or the destruction of valuable equipment. The thermal expansion of materials can be a major roadblock for building and designing, however, many application processes and technologies have been designed with thermal expansion as a fundamental component of function.

Figure 4: Expansion joint on a bridge
Barron, T.H.K., Collins, J.C., & White, G.K. (1980). Thermal expansion of solids at low temperatures. Advances in physics, 29(4), 609-730. https://doi.org/10.1080/00018738000101426
Figure 1 – The engineering toolbox, https://www.engineeringtoolbox.com/linear-expansion-coefficients-d_95.html
Figure 2 and 3 – X-Engineer, https://x-engineer.org/undergraduate-engineering/physics/thermodynamics/calculate-thermal-expansion/
Figure 4 – https://en.wikipedia.org/wiki/Expansion_joint#/media/File:BridgeExpansionJoint.jpg
In thermodynamics, CTE stands for Coefficient of Thermal Expansion. The coefficient of thermal expansion is a measure of how much a material expands or contracts when its temperature changes.
There are different types of thermal expansion coefficients:
Unless otherwise specified, CTE typically refers to the linear coefficient of thermal expansion
Author: Cole Boucher, Junior Technical Writer at Thermtest