May 3, 2024
July 7, 2022
June 24, 2022
January 24, 2022
October 28, 2021
July 8, 2019
November 26, 2018
September 22, 2017
June 9, 2017
September 27, 2017
July 24, 2017
September 22, 2017
September 27, 2017
November 26, 2018
January 30, 2019
In previous blogs, I have provided a “few” constructive tips on what one may describe as “the “essentials or basics” of the subject of the measurement of thermal transport properties associated with applications of materials. These, I trust, have convinced you that understanding the subject of measurement and application of thermal conductivity and its appropriate associated terms is a far more complex enterprise than retaining an original belief of being a simple experimental exercise based on a specimen with its ends at different temperatures,
This is due principally to the property being dependent on numerous additional parameters and factors, including specimen size and form, homogeneity, mean temperature, temperature difference, and environmental gas. Furthermore, the limits of accuracy and precision levels of the measured property, which are found in some cases to be temperature range dependent, become an important factor. This is especially relevant in consideration of the successful economic operation and performance of a designed system, whether it is for cryogenic or high-temperature operation where a 5% error in the design value of the material involved can result in a difference in costs of millions.
The earlier blogs indicate that there are two distinct options of acceptable proven methods available for the measurement of the thermal transport of the property resulting in choosing between one of several individual forms of steady-state techniques and one of two or three transient “one size fits all” methods that are available. To me, this decision of choice is comparable to that of having dinner at a restaurant and ordering from the a la carte or table d’hote menus.
From experience over many years, I have satisfied the requirements and needs for reliable property measurements of international user clients from within a spectrum containing governments, industries, and academia. This has resulted in developing and subsequently following a collated list of what I have considered essential factors that are directly relevant to any decision on the choice of method. These I have summarized and termed “golden rules” as follows:
1. Report ALL available relevant descriptive information (e.g., constituents, form composition, homogeneity, porosity, density, heat treatment, etc.) for identification of both the material and specimen,
2. Ensure that the model and associated experimental apparatus for a method has been verified independently as appropriate to address the test requirements,
3. A measured thermal property value applies ONLY to the specimen form and environmental conditions and assumed to be representative of the material or system,
4. A temperature sensor measures ONLY ITS OWN temperature; it is the responsibility of the experimentalist to ensure, not assume, that it is representative for the positioned object in the measurement conditions,
5. When measuring the property of an electrical conductor, it is ESSENTIAL that the electrical resistivity be measured, preferably simultaneously, over the same temperature range, with a repeat value at room temperature,
6. Use experience and history to identify what is or could be WRONG prior to acceptance that a measurement is correct,
7. The customer is NOT ALWAYS RIGHT.
As an exercise to explore this creed, let us suppose that one is provided with a new “material,” for which the thermal properties are unknown and need to be determined over all or parts of an application range of 10k to 800k. In addition, it is available in a reasonable amount for testing by any recognized current method, with the proviso that the measured property must have an accuracy level of +/-5% or better? Although there are many proposed methods available for this task, various factors including, specimen size and form, simplicity and speed of operation, questionable claims of accuracy, and cost have reduced the list to a relatively small number of current “standard” techniques, mostly for solids in some form and upon which an appropriate decision on selection can be made.
As discussed previously, for the three orders of magnitude of current applications’ temperature, the total range of thermal conductivity of all materials in their various types is at least six orders of magnitude. This varies from that for a homogeneous dense solid, such as a metal or ceramic or polymer-based solid, to a highly porous inhomogeneous mass of a fibrous, cellular, or particulate material of a thermal insulation from (1000+ to 0.01 W/m.k). However, within this range, various sub-groups include ceramic-based forms (approximately 1 to 100), polymer based (approx. 0.1 to 1), plus many types of graphite, carbon, composite and layered systems (approx.1 to 100). The other factor is the property value change with a temperature that can increase, decrease, or as a pure metal, do both with a peak at an intermediate temperature.
Following the golden rules, the first decision is to classify the basic material to establish the property range to be measured. A simple test of touching the surface will indicate whether it is a good or poor thermal conductor by feeling cold to warm. Over time, personal experience with different materials enables one to judge intermediate levels of both. It is particularly useful for indicating anisotropy in properties such as the 7:3:1 difference for the gallium crystal axes. However, the surface condition can influence the response and needs to be recognized when consideration is applied to a measurement
In addition, it is essential that sufficient detailed information must be provided or otherwise obtained to identify the material and specimen in detail. This is probably obvious but is not always recognized and subsequently reported in full in any published report or paper such that it can enable verification and judgment of the efficacy of any measured value. The absence of such descriptive support data does not provide an opportunity for such judgment to be made or allow for further evaluation to support the measurement value or development of theories or relationships, for example relating to the effects of temperature or amount or size of a particular constituent. It also becomes an important factor relating to item six above, as discussed later.
This latter issue is the biggest disappointment and a bone of contention of Professor Yeram Touloukian and his many colleagues at TPRC (now CINDAS), at Purdue University, who have devoted so much effort and time to the task of compilation and evaluation of published data for materials that are manifested in the large blue multi-volumed Thermal Properties of Matter published by Plenum Press and which is now being digitized for general-purpose especially for experimentalists as a means to compare or justify their own measurements. Once the form and property range has been determined, the next decision is the choice of an appropriate method.

Figure 1. Yeram S. Touloukian
Any method in this subject is the experimental representation of a model-based equation developed to describe the temperature distribution in a semi-infinite body during the change or at equilibrium following heat application. The chief issue in the model of basic steady-state apparatus design becomes the optimization of the geometry with respect to equilibrium times, heat dissipation, radiation transfer, and accuracy. Apparatus for both longitudinal and radial heat flow methods utilize a large specimen system with definite configurations plus appropriate guarding to ensure no or minimal heat loss or gain between the heater and the heat sink. The results, where heat losses can be quantified if they are suspected, are obtained from the measured temperature gradient at equilibrium and appropriate linear or radial dimensions. Significantly these are all measured values that allow for direct development of a reliable evaluation of the accuracy and precision levels. Thus, all thermocouples must be fixed solidly in position in or on the specimen to satisfy the fourth golden rule.
In contrast, transient methods differ completely as they address the variation of temperature distribution with time. This involves a differential heat flow equation where both time and space variables are important. Furthermore, there is a profusion of models for such techniques. Each has a different set of boundary conditions with a unique solution that results in an extra version of a specific method. Another significant feature is the manner of treatment of heat losses that can either be considered negligible due to the short times involved or by addressed by the inclusion of an extra term or constant in the equation that subsequently can be eliminated by additional measurement under different experimental conditions. However, these factors illustrate that with various choices of unquantified parameters available, they are a source of potential uncertainty, affecting the accuracy levels.
These techniques normally determine thermal diffusivity from which, with values of density and specific heat, the thermal conductivity can be derived. However, under certain experimental conditions, thermal conductivity can be obtained directly, but not all models are equivalent where precision and accuracy are considered. For example, the models for the transient line source and transient plane source techniques are similar and based on uniform symmetric heat flow developed within the specimen, but in the modified version of the latter, the heat flow is asymmetric and developed at the specimen surface so does not follow the model. In summary, transient techniques are relatively simple in the form of apparatus and procedure. They are fast in operation and use relatively small amounts and forms of homogeneous material as a specimen. As discussed in the previous blog, due to the continually increasing need for thermal property data for materials of all types, they have become popular, especially in the form of a commercial automated “one size fits all.”
The Fourier description of heat flow addresses only the dominant conduction mode of heat transfer in isotropic materials. A measurement method results in a unique quantified thermal conductance value for the test specimen only. Assuming the specimen is dense and homogeneous and introducing the length dimension in the equation, the measured value becomes a thermal conductivity. Thus, for all heterogeneous and lower density materials where heat transfer includes the effects of convection and/or radiation, particularly at high temperatures becomes significant, it is now recognized that the measured property is an apparent or effective thermal conductivity. In addition, convection can occur in low-density porous materials when subjected to the use of large temperature differences temperatures with upward vertical heat flow.
Both the measurement of “thermal conductivity” and the interpretation of measured result must now include and allow for such effects that indicate that the property can only be viewed as specimen material and environment dependent. Consequently, these more rigorous limits have now provided added responsibilities to those working in the thermal measurement community, especially in deciding the best or most appropriate method to attain the desired precision and accuracy. During my many years of active experience as a supplier of information, I am sure that the most common request that I have received has been a simple “please measure the thermal conductivity of my material(s)Z, at some fixed temperature or over the temperature X and Y.” Furthermore, I am sure that the client expected a simple reply but was totally surprised to be grilled with questions concerning the above factors. It is a prime example that illustrates the reasons for golden rules six and seven.
On further examination, if the material is known or considered to be a relatively “pure” homogeneous solid, the requested measurement can be carried out by undertaking measurements on materials in the top two sub-groups by either a steady-state longitudinal rod or comparative slab method or a transient line or plane source technique. For the former, the specimen will be of a definite form of relatively large size. For the transient methods, it is usually a plate or disc of relatively small dimensions. If the property is required over a temperature range, the measurements should be made at regular appropriate mean temperature intervals for the extent of the range and with a temperature difference in the specimen of the order of 10 to 30k for the steady-state method.
The accuracy levels of each of these methods are claimed and shown to be at or above the required range, and where possible a suitable effort should be made to show that the measured values are within the acceptable level. This subject can be addressed from theoretical considerations. According to the basic theory of conduction by phonons in “pure” solids above the Debye temperature of the material, the thermal conductivity is inversely proportional to the absolute temperature. This can be utilized if the Debye temperature is known for the specimen material and sufficient data points are available to illustrate such a relationship. Unfortunately, they cannot be used for a measurement at a single temperature or on heterogeneous solids.
However, for metals and alloys, confidence in measured values is more definitely illustrated by using the Wiedemann-Franz law based on conduction by electrons. This states that the ratio of the electronic contribution of the thermal conductivity to a metal’s electrical conductivity is proportional to the temperature and was taken stage by further by showing that it was a constant, the Lorenz Number, L, at all temperatures. Modification by the inclusion of a constant for the phonon component (due to impurities, grain boundaries, etc.) has provided relationships for numerous metal-based alloy systems from aluminium to zirconium that can be used to derive values of thermal conductivity at the 5% level for alloys that do not involve significant amounts of carbon and silicon. Measurement of electrical resistivity is a simple one to make, and a measurement of both properties provides an internal assessment of the efficacy of the measurement when L is found to be close to the expected value, thus fully justifying the fifth golden rule.
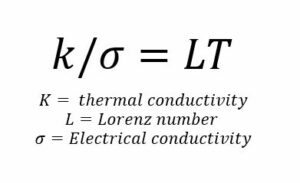
Figure 2. Wiedemann-Franz law equation
All that remains is a large group of materials and systems that include all thermal insulations and many rigid less-homogeneous low thermal conductivity (0,01 to 10 W/m.k) porous cellular, fibrous, particulate, and layered forms of solids. For thermal insulations, decisions on the measurement method have been influenced by experience gained using the ISO standard hot plate and heat flow meter. This has been indicated to attain 5% accuracy. The specimen representative area representative shall be greater than 10cm and 60cm square or diameter for specimens up to 7.5 and 15cm thick, respectively. Such requirements eliminate or seriously restrict the use of current transient methods due to the probe unit’s small surface area.
However, both the transient and the comparative slab steady-state methods can be used for the other porous solids, so take due to ensure that the specimen size is representative of the material.
Renaissance man