Thermal Conductivity – Resistance: Materials

Safety: Please take all necessary safety precautions

Abstract

Thermal Conductivity is an important material property in industry and daily situations like knowing what to choose in cookware or the proper clothing worn to leave the house. This property is described in units of Watts per meter Kelvin and at steady state can be calculated via a measurement of thermal resistance. Both Thermal Conductivity and Thermal Resistance will affect the amount of heat which passes through a system. In this experiment, a simple set-up will be employed to observe the change in heat flow.

Introduction

The goal of this experiment is to demonstrate the effect which varying thermal conductivities have on the heat flow through a given material. Ultimately this will provide a better understanding of both thermal conductivity and thermal resistance

Background Information and Equations

Background Information

Thermal Conductivity is a measure of a materials ability to transfer heat through itself and is one of the 3 variables in Thermal resistance. Thermal Resistance is analogous to Electrical Resistance in that it is inversely proportional to the flow of heat. In a laboratory setting, thermal resistance is calculated under specific circumstances allowing for thermal conductivity to then be derived from the obtained results.

Heat Flow Equation Q = ΔT / RΘ

• Q = Heat flow in Watts
• ΔT = Temperature difference in Degrees Celsius
• RΘ = Thermal Resistance (l / k ⋅ A)
• l = Length of a material in Meters
• k = Thermal conductivity constant in W/m-K
• A = Surface area in meters squared

This experiment will vary the bolded constant via different samples.

This experiment was designed to compare thermal conductivities thus surface area, length and temperature difference must remain the same in every test. One may use non-metals for this experiment however, may run the risk of lengthy testing time or potential incompletion. It is therefore suggested that metals be used. A listing of common metals may be found in the comparison section.

Materials

Procedure

1. 1. Obtain two beakers (similar or different size), fill one with water and place it on the hot plate.
   2. Place the other beaker on object of similar size to the hotplate as to make the lips of both beakers at the same height (or use a taller beaker)
   3. Bend all the wires 90° on both ends creating 50mm arms and ensure that 1m of straight wire is maintained
   4. Ensure that the bent end of the wire is immersed in the water
   5. Place all three wires of choice on the lips of both beakers as to connect both beakers

1. Use a marker to mark each wire every 200mm or if using candles, melt the bottom of each candle using some source of heat and place the candles at 200mm intervals along the wire
2. Heat the water using the hot plate for 15 minutes and then take temperature readings at each 200mm intervals

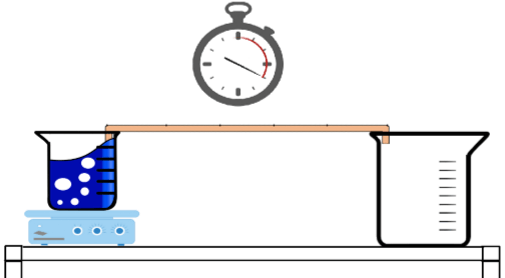
*shorter wires may be used for a faster experiment time if needed, simply make a measurement at every 1/5th of the wire*

Observation

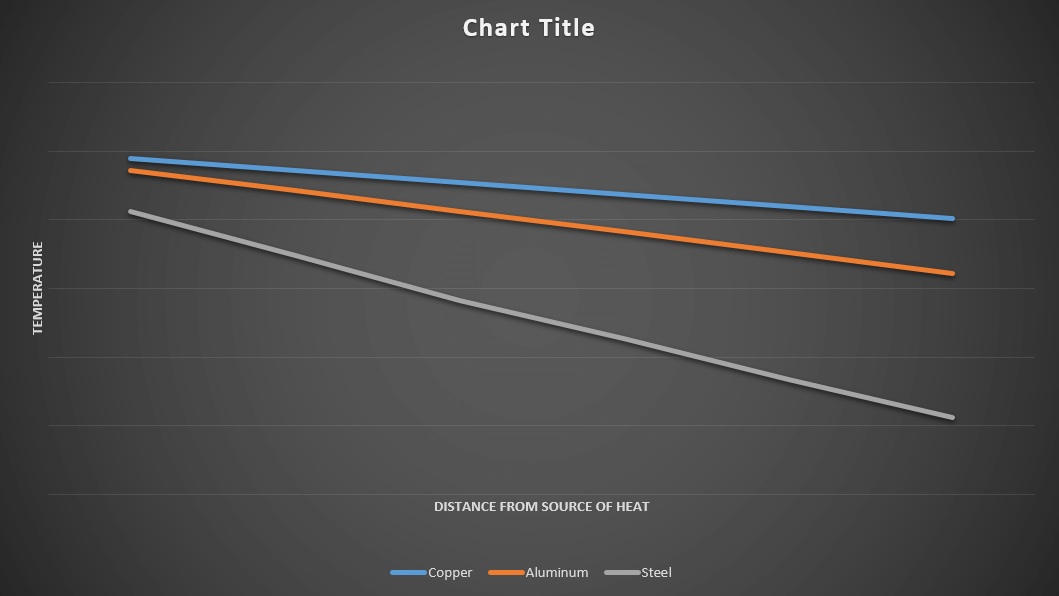
There are two ways one can visualize the progression of the heat through the wires. Initially, one can observe the degree to which the candles melted at each 200mm interval. The wire with the highest thermal conductivity will have the greatest severity of melted candle, whereas; the wire with the lowest thermal conductivity will have the weakest severity of melted candles near the heat source. One can also use an Infrared Thermometer to measure each 200mm interval along the wire and plot the recorded data against the distance from the boiling water. The plot with the greatest difference from between 0mm and 1000mm will most likely be the worst thermal conductor. The produced plot should look similar to the one below.

Comparison

Below is a list of metals along with their thermal conductivity value. The higher the thermal conductivity value, the better thermal conductor that material will be.

*For other thermal Conductivity Value visit: https://thermtest.com/materials-database

Conclusion

Metals transfer heat via accumulated energy in the free electrons of the metal atoms, these electrons will collide with one another transferring their kinetic energy. This billiard like interaction will propagate throughout the metal until the energy is uniformly spread. Copper is usually considered the best thermal conductor on a thermal conductivity to price ratio. The only metal surpassing Copper is Silver with a thermal conductivity of 429.77 W/m-K. With this in mind, it would be to no surprise if the copper wire is found to have the have the highest temperature across all 200mm intervals and the highest degree of melted candles. Part Two of this experiment series will look at the variations in thermal conductivity due to length of a given material.

For further Information, visit:
https://thermtest.com/what-is-thermal-conductivity
https://thermtest.com/thermal-resources/energy2d-heat-transfer-simulations/
https://en.wikipedia.org/wiki/Thermal_conductivity