Using Heat flux to determine the length of an aluminum rod of unknown length

Abstract

Heat flux is described as the amount of energy (in joules) which passes a through a given surface over some unit of time. Heat flux is usually calculated in Watts per meter squared and can be calculated using the product of the thermal conductivity constant of aluminum and the temperature difference over the length of a sample of aluminum. This experiment will use the Heat flux through an aluminum rod to then determine the length of an aluminum rod with an unknown length.

Hypothesis

Using the heat flux of an aluminum rod of known length, a prediction can be made of the length of another aluminum rod of unknown length.

Background

• Q = Heat flux (W/m²)
• k = Thermal conductivity constant of a given material (W/m⋅K)
• For aluminum = 225.94 (W/m⋅K)
• Δx = Length of the rod(m)
• T₁ = Temperature of the Heat source (°C)
• T₂ = Temperature of the tip of the rod(°C)
• r = radius of the rod(m)
• d = diameter of the rod(m)

Heat flux equation: Q = [k⋅(T₁-T₂)]/Δx
Rearranged for Δx: Δx = [A⋅k⋅(T₁-T₂)]/q

Materials

• 2 Styrofoam blocks (can be found joann.com, ~2.00$)
• 2 Aluminum rods of same diameter, one of unknown length and one of known length (can be found on amazon, ~ $13)
• Hot plate (~$15)
• Beaker (250ml or 500ml ~$12.00 or less)
• Lab stand (~$20)
• Stopwatch (~$5)
• Thermocouple and thermometer (found on omega.ca and amazon, ~$20)
• Ruler ($1)
• Water

Unless otherwise stated, all of the stated materials may be found on Amazon. The total cost will be around $100

Procedure

Phase 1:

1. Pour enough water to fill three quarters (187.5ml or 375ml) of your beaker and bring the water to the desired temperature (recommended: 70°C)
2. Measure the diameter and length of the aluminum rod and pierce a hole in the Styrofoam block ensuring that the aluminum rod fits tightly within it
3. Ensure 2-3mm of aluminum rod is exposed on one end of the Styrofoam block
4. Attach the thermocouple to the free end of the aluminum rod
5. Place the aluminum rod and Styrofoam block into the hot water bath and record the temperature of the hot water bath submerging the exposed rod and 2-3mm of the Styrofoam block
6. Ensure the block is clamped to the lab stand in order to avoid falling of moving
7. Maintain the water bath for 2 minutes at a constant temperature
8. Record the temperature once 2 minutes has passed and remove the Styrofoam block from the bath
9. Using the temperature acquired calculate T₁ – _T2
10. Calculate Q using the thermal conductivity constant (k), temperature difference (T₁ – _T2) and the length of the aluminum rod (Δx).

Phase 2:

1. Repeat phase 1 using the second rod of unknown length (important note: ensure the same area of aluminum rod is exposed to the hot water bath)
2. Acquire the new T₁ – _T2
3. Using the previously calculated heat flux, thermal conductivity constant and new T₁ – _T2 calculate the length of the aluminum rod with the heat flux equation rearranged for Δ
4. Measure the actual length of the aluminum rod using a ruler and compare the results

Considerations

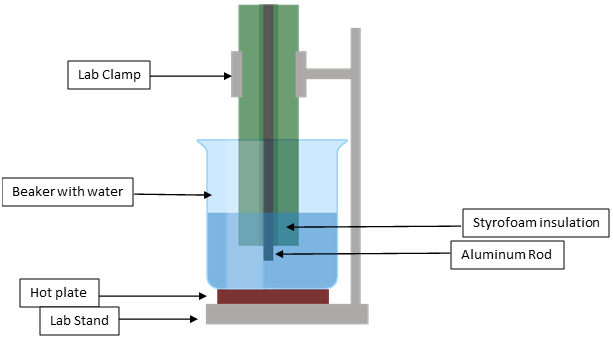
For the Heat flux to be considered the same for both rods, the exact same procedure must be followed. Leaving the rod in the hot water bath for longer than the other rod will decrease the Heat flux via an increased T2. The same is also true for the opposite, should the one rod be left in the hot water bath for a shorter period, the T2 will be smaller and thus the Heat flux greater. A substitute for Styrofoam may be used in this experiment; however, an insulator with similar properties should be used to prevent heat loss from the aluminum rod and skew the T2.

The equation employed in this experiment work under the assumption that the system is defined as steady state. Therefore, on small scale (rods smaller than ~30 cm and differing less than ~10 cm) the calculations will hold. More precise instrumentation should be used if larger scale experiments were to be performed.

Conclusion

Heat flux is a measure of energy passing through an area over a given time regardless of the length of that material. Should the length of a rod increase in length, the temperature at the end of that material will decrease and vice versa if exposed to the same amount of heat.

For further information on heat flux and thermal conductivity constants of other materials visit:

• https://thermtest.com/materials-database
• http://www.physicsclassroom.com/class/thermalP/Lesson-1/Rates-of-Heat-Transfer
• https://en.wikipedia.org/wiki/Heat_flux