EN

Thermal Conductivity Meter: Searle’s Apparatus

1.0 Introduction

George Frederick Charles Searle was born December 3rd, 1864 and was a British Physicist and Lecturer. Searle first began working at the University of Cambridge in 1888 at the age of 24 under the supervision of J. J. Thompson. He continued his work for another 55 years. Searle is best known for his contribution to the research on the velocity dependence of electrostatic mass which played an important role in the formulation of Einstein’s special theory of relativity. Along with these achievements, the Searle’s Bar experiment was produced, a simple and affordable way to calculate the thermal conductivity of good thermal conductors.

2.0 Background Information and Relevant Equations

2.1 Background Information

It is important to note that for this experiment to be successful, the rod being measured must be a good thermal conductor.
Most metals are considered good thermal conductors thus any metal rod would be suitable for this experiment. Common materials with high enough thermal conductivities include: Copper, Stainless Steel and aluminum.

2.2 Relevant equations and Constants

Specific Heat of Water = 4.18 Joules/(gram⋅°K)

Energy absorption of water (Q) = c ⋅ m ⋅ ΔT

  • c = Specific heat of water in Joules per gram ⋅ Kelvin
  • Q = Energy Absorbed by a given sample of Water in Joules
  • m = Mass of a sample of water in grams
  • ΔT = Temperature difference of a given sample of water exposed to some source of heat

Heat Flow Rate (Q) = k ⋅ A ⋅ (T1-T2) / d

  • k = Thermal Conductivity in Watts/Meter-Kelvin
  • A = Area in meters squared(m2)
  • T1 and T2 = Temperatures in Kelvin
  • d = Distance which the heat travels in meters

Cross sectional Area = πD2 / 4 OR πr2

3.0 Materials, Experimental Set up and Procedure

3.1 Materials

Materials Required Price Location of Purchase
Copper Tubing $7 Amazon.com
Steam Chamber/Maker Varying Price Varying Locations
Thermometer x4 $10 x4 = $40 Amazon.com
Beakers (500ml)x2 $4 Amazon.com
Tubing $3 Amazon.com
Insulating Material(Cotton or Felt) $10 Amazon.com
Vernier Caliper $10 Amazon.com
Metal Rod Varying Price Speedymetals.com
Digital Scale $15 Amazon.com
Total $98  

*For how to make your own Steam Chamber, See Lee’s Disc Experiment*

3.2 Experimental Setup

  1. A hole should be made in the steam chamber equal to the cross-sectional area of the rod whose thermal conductivity is being calculated. The interface between the rod and steam chamber can be welded together to prevent dislodging.
  2. Two holes should be made into the metal rod in line with each other along the length of the rod. The first two thermometers will be placed in these holes thus if there are any air pockets, thermal grease (thermal interface material) can be placed in the holes.
  3. The copper tubing should be tightly wrapped around the rod and connected on either end by tubing. Should no Y-neck adaptor be available, a hole can be made in the tubing (if plastic or rubber) to allow entry of the thermometer in order to measure the incoming and outgoing water temperatures.
  4. A thermal insulating material should be wrapped around the metal rod in order to prevent heat loss by the rod to the environment.

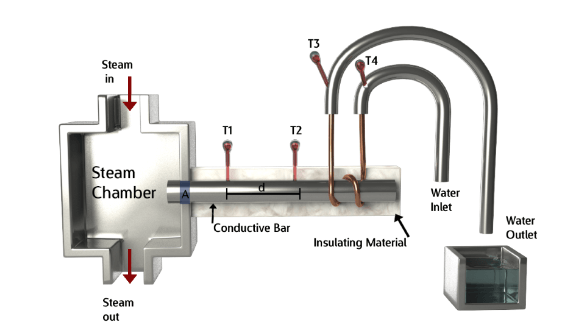
Thermal Conductivity Apparatus Searle’s Setup Thermtest Resources

The thermal conductivity apparatus resulting setup should resemble the above figure.

3.3 Procedure

  1. Using a Vernier caliper or other measuring tool calculate the cross-sectional area (A) of the metal rod and the distance (d) between thermometers 1 and 2
  2. Pre-weigh the 2 500ml Beakers
  3. Turn on the water inlet tube and the steam generator.
  4. Allow the system to reach steady state (no change in any temperature for 5-10 minutes)
  5. Once steady state reach, record the temperature displayed on each thermometer (T1, T2, T3 and T4)
  6. Collect a desired amount of water (between 500ml-1000ml) over a given time period (t)
  7. Weigh the beakers filled with water and subtract the weight of the beaker to determine the mass of water passing through the copper tubing over a given time (t)

4.0 Calculations & Comparison

4.1 Calculations

The Rate of Heat transfer between thermometers 1 and 2 over a given distance d will be given by the formula:

  • Q / t = k ⋅ A ⋅ (T1 – T2) / d
    (1)

This Formula can be rearranged to produce the following:

  • k = Q ⋅ d / πr2 (T1 – T2) ⋅ t
    (2)

The amount of energy absorbed by the water is given by:

  • Q = c ⋅ m ⋅ ΔT
    (3)

With this formula in mind, Q of equation (2) can be replaced by the equation (3) producing the following:

  • K = m ⋅ c ⋅ (T3-T4) ⋅ d / πr2 (T1 – T2) ⋅ t
    (4)

A simple insertion of the values experimentally obtained can be performed to calculate the thermal conductivity of the metal in question

4.2 Experimentally determined Thermal Conductivity values for comparison

Once calculated, the experimental thermal conductivity constant of a given material can be compared to the experimental thermal conductivities obtained by highly specialized labs.

Type of Material Thermal Conductivity Constant (W/mK)
Copper 397.48
Aluminum 225.94
Bronze 188.28
Iron 71.965

*Thermal Conductivity values taken from the Thermtest thermal properties database, for more Thermal Conductivity values visit: https://thermtest.com/materials-database

5. Conclusion

Unlike the Lee’s Disc experiment, the Searle’s Bar experiment is intentionally designed to calculate the thermal conductivity of materials with high thermal conductivities. Metals are generally considered the better thermal conductors due to their highly order molecular arrangement however there are some non-metals which can surpass metals in thermal conductivity such as Graphene.
Using this list of instructions, anyone can become a thermal physicist and calculate the thermal conductivity of various metals for an affordable price.
Web Resources for further Information:
https://thermtest.com/thermal-resources/build-your-own/lees-disc/
https://thermtest.com/applications/graphite-sheets-thermal-conductivity/
https://en.wikipedia.org/wiki/Searle%27s_bar_method

To make your own simulation:
https://thermtest.com/thermal-resources/energy2d-heat-transfer-simulations/

Click here to read the disclaimer

Thermtest is furnishing this item "as is". Thermtest does not provide any warranty of the item whatsoever, whether express, implied, or statutory, including, but not limited to, any warranty of merchantability or fitness for a particular purpose or any warranty that the contents of the item will be error-free. In no respect shall Thermtest incur any liability for any damages, including, but limited to, direct, indirect, special, or consequential damages arising out of, resulting from, or any way connected to the use of the item, whether or not based upon warranty, contract, tort, or otherwise; whether or not injury was sustained by persons or property or otherwise; and whether or not loss was sustained from, or arose out of, the results of, the item, or any services that may be provided by Thermtest.

    How can we make this page better for you?

    Can’t find the right product for your testing?

    Send us an inquiry now
    Linkedin