Thermal Diffusivity – An Overview

Introduction

The concept of Thermal diffusivity is frequently confused with that of thermal conductivity. They are closely related concepts; however, thermal conductivity appears to be more prevalent in the scientific community. Even as the less popular of the two heat transfer measurements, thermal diffusivity still plays an important role in influencing the movement and behavior of heat.

Thermal diffusivity is a measure of the rate at which heat disperses throughout an object or body. Thermal conductivity is a measure of how easily one atom or molecule of a material accepts or gives away heat. The main idea behind thermal diffusivity is the rate at which heat diffuses throughout a material.

Expressions for Thermal Diffusion

Thermal conductance can also be viewed as a factor of thermal diffusion. A material that is said to conduct heat efficiently must also have effective heat diffusion properties in order to facilitate heat transfer. Density is another factor of thermal diffusion. A material with a high density is composed of atoms/molecules packed tightly together. A higher density can limit the speed and distance that heat can travel through the object. An increase in density can be imagined as a highway with more toll booths, where the cars are energy quanta in the form of heat.

The specific heat capacity is the last relevant factor when just regarding solids, as this quantity relates to how much heat can be held by one atom/molecule at a time. This can be pictured as a stoplight that is more likely to change as more cars come to a stop at it. Increasing the specific heat of the material would be like lessening the positive effect that every car stopped at the light has on the likelihood of the light changing to green. Fluids are also affected by convection, which is the movement of the atoms/molecules caused by heating. Convection impacts heat transfer and makes thermal diffusivity much harder to mathematically model. However, if the focus is on solids, a simpler representation can be formed.

\[ a = \frac{k}{(pc)} \]

Where k is the thermal conductivity, p is the density, and c is the specific heat capacity at constant pressure. pc is often referred to as the volumetric heat capacity.

For an individual with a background in mathematics or a related field, this concept might be somewhat familiar. This can be attributed to a rather useful form of equation that describes the diffusion of any property through a consistent medium. This form of equation is called the ‘heat equation’ because heat diffusion is its most common use.

\[ \dot{u} = a \nabla^2 u \]   ‘Heat Equation’

Where \[ u \] is a measure of some property, \[ \dot{u} \] is its derivative with respect to time, and \[ \nabla^2 \] is its Laplace operator (the divergence of the gradient)

In the case of heat transfer through a homogeneous (uniform) body, \[ u \] could represent temperature and α would be the same as above.

\[ \frac{dT}{dt} = a \nabla^2 T \]

One benefit of this equation is that \[ \nabla^2 \] can often be written independently of any coordinate system. In this form it is clear to see that thermal diffusivity is a scaling factor, meaning it directly controls the speed at which temperature changes.

Experimental Methods of Finding the Thermal Diffusivity

It is possible for the thermal diffusivity to be measured alongside thermal conductivity if the density is known. One method would be the Searle’s bar experiment, which gives an equation for thermal conductivity

\[ k = cmd \frac{(T3-T4)}{A(T1-T2)} \]

If the following equation is substituted into the thermal diffusion equation without an initial calculation, then the specific heat capacity would not need to be known.

Improvements in modern technology have created more accurate methods for determining the thermal diffusivity of an object. The flash method is a relatively new way to measure thermal diffusivity. In this method, a small sample of the material with pre-determined dimensions is coated in black paint that is designed to make the sample behave as a black box. A face of the sample is then struck with a short duration of very intense light. Knowing the wavelength and intensity of this light, the amount of energy it imparts into the sample is easily estimated with high accuracy. The opposite face of the sample is in contact with a thermocouple which measures the temperature of that face. An oscilloscope plots the measured temperature with respect to time. The thermal diffusivity can then be found through the shape of the graph by rearranging the heat equation.

\[ a = \frac{dT}{dt} \frac{1}{\nabla^2 T} \]

Applications of Thermal Diffusivity

Many industries rely on thermal diffusivity to determine the most suitable materials to optimize efficient heat flow. Insulation is an example of a material that requires a low thermal diffusivity so that a minimal amount of heat is passing through it at any one time. A heat sink is an appliance that is designed to carry the heat out and away from another piece of equipment. A heat sink is required to have a very high thermal diffusivity that enables the quick transport of the heat. If slow heat transfer were to occur, the area accepting the heat would heat up and not permit as much heat flow per unit time. Heat sinks are used in almost every piece of electrical equipment. An increase in temperature in certain components can lead to an increased electrical resistance and unexpected behavior.

Technologies such as refrigeration, heating, machining, and architecture all hold thermal diffusivity to a paramount importance. Outlined below is a list of the materials with the highest and lowest thermal diffusivities. This list is courtesy of Thermtest’s extensive materials thermal properties database.

Material	Thermal Conductivity (W/m•K)	Thermal Diffusivity (mm2/s)	Specific Heat Capacity (J/kg•K)	Material Density (kg/m3)
Iodine (Solid)	0.004	0	218	4930
Ammonia (NH3) (Liquid Under Pressure)	0.05	0.02	4686	618
Ethyl Vinyl Acetate	0.075	0.03	2301	1200
Tetradecafluorohexane	0.057	0.0308	1100	1680
Urea-Formaldehyde Molded	0.126	0.05	1674	1500
Polyvinylidene Fluoride (Kynar)	0.126	0.05	1381	1760
Polyvinyl Butyral	0.084	0.05	1674	1100
Butyl Rubber	0.088	0.05	1966	900
R12 (Dichlorofluoromethane)	0.07	0.0531	886	1488
R134a (Tetrafluoroethane)	0.1	0.0566	1280	1380

Table 1: Measurements of Thermal Conductivity, Lowest Thermal Diffusivity, Specific Heat Capacity, and Material Density.

Material	Thermal Conductivity (W/m•K)	Thermal Diffusivity (mm2/s)	Specific Heat Capacity (J/kg•K)	Material Density (kg/m3)
Graphite Sheet 100 Um (In-Plane)	700	968	850	850
Graphite Sheet 25 Um (In-Plane)	1600	896	850	2100
Graphite Sheet 70 Um (In-Plane)	800	855	850	1100
Carbon Diamond Gem Quality Type 1	543.92	306	506	3510
Silicon Carbide (SiC) (Single Xtal)	489.53	225	678	3210
Silver	426.77	172	236	10500
Helium (Gas)	0.15	164	5188	0.177
Potassium	97.069	150	753	862
Hydrogen (Gas)	0.186	145	14230	0.0899
Silver Alloys Sterling And Coin	359.82	137	251	10500

Table 2: Measurements of Thermal Conductivity, Highest Thermal Diffusivity, Specific Heat Capacity, and Material Density.

Reference

“On thermal diffusivity” – Agustin Salazar – May 2003 European Journal of Physics 24(4):351; 10.1088/0143-0807/24/4/353 – https://www.researchgate.net/publication/231038795_On_thermal_diffusivity

“Flash Method of Determining Thermal Diffusivity, Heat Capacity, and Thermal Conductivity” – W. J. Parker, R. J. Jenkins, C. P. Butler, and G. L. Abbott – Journal of Applied Physics 32, 1679 (1961); 10.1063/1.1728417 – https://aip.scitation.org/doi/abs/10.1063/1.1728417

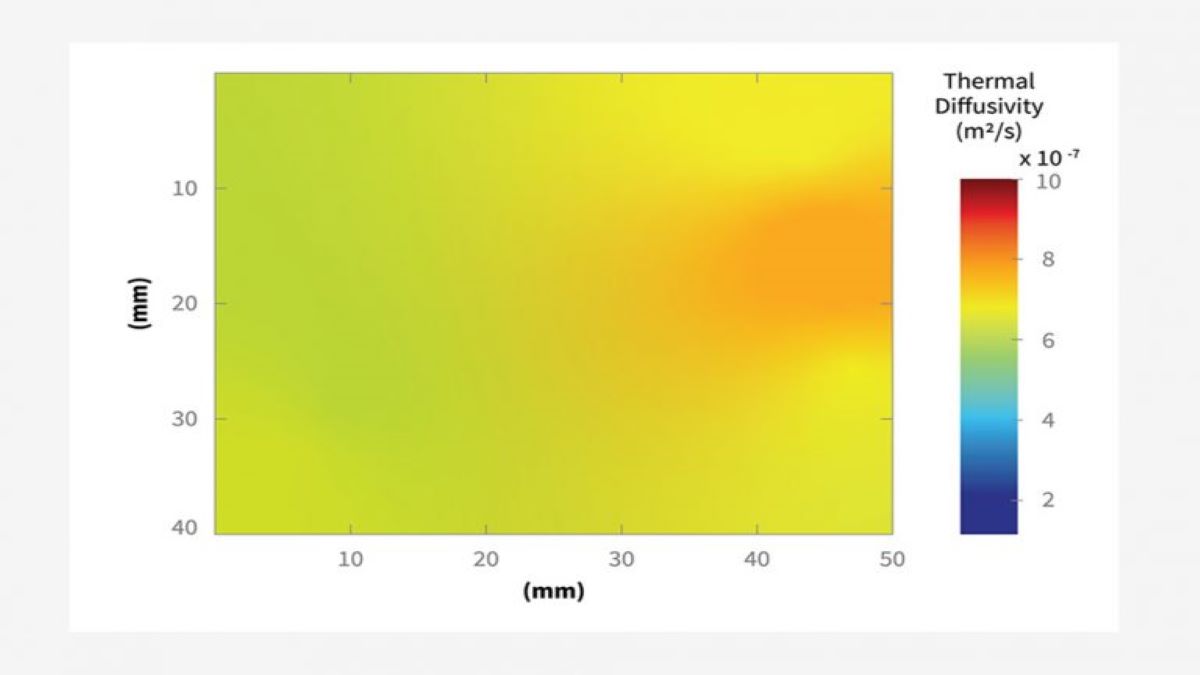
“Thermal Diffusivity Mapping of Graphene-Based Polymer Nanocomposites” – Matthieu Gresil, Zixin Wang, Quentin-Arthur Poutrel & Constantinos Soutis – Scientific Reports | 7: 5536; 10.1038/s41598-017-05866-0 – https://www.nature.com/articles/s41598-017-05866-0.pdf

MATERIALS THERMAL PROPERTIES DATABASE – https://thermtest.com/materials-database

Image Sources:

https://www.reenergizeco.com/wp-content/uploads/2019/01/improve-home-insulation.jpg
https://images.freeimages.com/images/large-previews/83d/heatsink-1541845.jpg

Author: Cole Boucher, Junior Technical Writer at Thermtest