Join us at the International Thermal Conductivity Conference (ITCC) and the International Thermal Expansion Symposium (ITES).
February 16, 2024
May 4, 2021
September 26, 2019
May 25, 2021
October 30, 2019

December 12, 2017
Thermtest is happy to introduce the new Thermal Resistance in Series Calculator. After inputting the thermal resistance and thickness of the material, the calculator outputs the thermal resistance of the composite.
As the name suggests, thermal resistance is a measurement of a temperature difference of a material’s ability to resist the flow of heat. Heat is energy that is transferred from one object or substance to another because of a difference in temperature between them. Heat flow is the movement of heat from the interior of Earth to the surface.
Thermal Resistivity is often described as the reciprocal of thermal conductance. The SI units are kelvins per watt or the equivalent degrees Celsius per watt. This thermal property greatly depends on the area, thickness, and thermal conductivity of a material.
Resistance increases by increasing the thickness of the material, and decreasing its area and thermal conductivity. Often times, heat flow and temperature can be determined from thermal resistance. This becomes useful in construction applications, when heat loss from electronics must be accounted for in building designs.
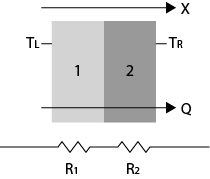
Figure 1. A structure composed of two materials with different resistances, where the heat flux through them (Q) is considered constant.
When the heat flux through multiple mediums is assumed constant, the thermal resistance “in series” can be determined. Thermal resistance can be compared to an electrical circuit model. In this case, heat flow is represented by current, temperatures are substituted with voltages, and resistances are expressed as resistors.
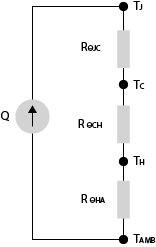
Figure 2. Thermal resistance represented as an electrical circuit. Current is replaced by heat flow (Q), voltages are represented as temperatures (T), and resistors are substituted for resistances (R).
The heat flow, or boundary temperatures of the system, can also be determined when an object’s resistance is known. In series, the heat flux through a composite material is considered constant, and the different series are equivalent to:
\[R = R_{1} + R_{2}\]
When the temperatures on each side of the composite material are known (\(T_{L}\) and \(T_{R}\)), the heat transfer rate is expressed as:
\[\dot{Q}=\frac{T_{L} {-} T_{R}}{R} = \frac{T_{L} {-} T_{R}}{R_{1} {+} R_{2}}\]
This thermal resistance equation can be applied to the “in series” composites, such as a wall surrounded by insulation, because \(\dot{Q}\) is constant across each component. The heat transfer of a composite material can be determined with the thermal resistance formula:
\[{Q}=\frac{T_{ \infty 1} {-} T_{1}}{R_{conv1}} = \frac{T_{1} {-} T_{2}}{R_{wall}}= \frac{T_{2} {-}T_{ \infty 2}}{R_{conv1}}\]
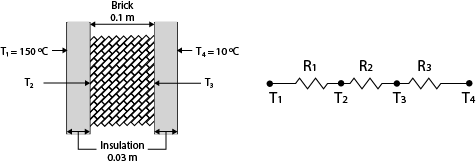
Figure 3. The thermal resistances (R) and temperatures (T) of a wall surrounded by insulation (left), modelled as an electrical current (right).
From which, the resistances of each component, \(R_{conv1}\), \(R_{wall}\), and \(R_{conv2}\) can be calculated using:
\[R_{total}=R_{conv1}+R_{wall}+R_{conv2}\]
After the total resistance of the system is known, the heat flow through the composite can be calculated from the heat flow equation. This includes the known boundary temperatures, as seen in the following equation.
\[Q = \frac{T_{ \infty 1}{-}T_{ \infty 2}}{R_{total}}\]The Resistance in Series Calculator is capable of easily determining the thermal resistance of composite materials. The calculator can also be used combination with Thermtest’s materials database, which includes the thermal properties of more than 1000 materials. This newly designed calculator provides a fast, simple, and accurate way to calculate the thermal resistance in series.
References
https://neutrium.net/heat_transfer/thermal-resistance/
http://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/node118.html