LIMITED TIME OFFER: Get a Free MTPS Sensor with Your MP Series Purchase – Offer Ends August 31, 2025!

En blogs anteriores, compartí ‘algunos’ consejos constructivos acerca de lo que se podría describir como ‘los puntos esenciales o básicos’ de la medición de las propiedades de transporte térmico asociadas con las aplicaciones de los materiales. Confío que logré convencerlos de que entender la medición y la aplicación de la conductividad térmica y los términos correctos asociados es una tarea mucho más compleja que creer que se trata de un simple ejercicio experimental basado en una muestra cuyos extremos exhiben diferentes temperaturas.
Principalmente, esto se debe a que la propiedad depende de numerosos parámetros y factores adicionales, entre ellos el tamaño y la forma de la muestra, la homogeneidad, la temperatura media, la diferencia de temperatura y el gas del medioambiente. Además, los límites del nivel de exactitud y precisión de la propiedad que se mide que, en ocasiones dependen del rango de temperatura, se vuelven un factor importante. Esto resulta especialmente relevante al considerar el rendimiento y comportamiento económico exitosos de un sistema diseñado, ya sea para una operación criogénica o de alta temperatura, donde un error del 5% en el valor del diseño del material en cuestión puede desencadenar una diferencia millonaria en los costos.
En los blogs anteriores se mostraba que existen dos opciones diferentes de métodos probados que son aceptables y están disponibles para la medición del transporte térmico de las propiedades, y que resultan de elegir entre una de varias opciones individuales de técnicas de estado estable y uno o dos métodos transitorios “universales” que se encuentran disponibles. En lo personal, creo que esta elección puede compararse con cenar en un restaurante y pedir menú a la carta o menú fijo.
Gracias a mi experiencia de muchos años, siempre he podido satisfacer los requisitos y las necesidades de mediciones confiables para los clientes internacionales en un amplio espectro de usuarios, entre ellos gobiernos, industrias y el sector académico. Esto me ha llevado a elaborar, y posteriormente, a trabajar con una lista de los que considero los factores esenciales que son pertinentes, de forma directa, para toda decisión sobre el método que se debe elegir. A continuación, los describiré bajo el nombre de “las reglas de oro”:
Como ejercicio para explorar esta creencia, supongamos que recibimos un ‘material’ nuevo, del que no conocemos sus propiedades térmicas y debemos determinarlas para un rango de aplicación total o parcial de 10 k a 800 k. Además, contamos con una cantidad razonable para realizar la prueba con cualquier método actual reconocido, con la condición de que la propiedad medida debe tener un nivel de exactitud de +/- 5% o superior. Si bien hay muchos métodos propuestos disponibles para realizar esta tarea, diversos factores, entre ellos el tamaño y la forma de la muestra, la simplicidad y la velocidad de la operación, cuestionamientos sobre la exactitud y el costo, han reducido la lista a un número relativamente pequeño de técnicas actuales ‘estándar’, mayormente para sólidos de alguna forma, y mediante las cuales se puede tomar una decisión adecuada sobre la selección.
Como mencioné anteriormente, para las tres órdenes de magnitud relativas a la temperatura actual de las aplicaciones, el rango total de conductividad térmica de todos los materiales en sus diversos tipos es de al menos seis órdenes de magnitud. Esto varía desde un sólido denso homogéneo, como un metal, una cerámica o un polímero, hasta una masa no homogénea altamente porosa de un material fibroso, celular o particulado con una aislación térmica de 1000+ a 0,01 W/m.k). Sin embargo, dentro de este rango, los diversos subgrupos incluyen formas basadas en cerámica (aproximadamente 1 de 100), en polímeros (aproximadamente 0,1 a 1), además de muchos otros sistemas de grafito, carbono, compuestos y en capas (aproximadamente 1 de 100). El otro factor a considerar es el cambio en el valor de las propiedades con una temperatura que puede subir, bajar, o hacer ambas cosas, como en el metal puro, y presentar un pico en una temperatura intermedia.
Cumpliendo con las reglas de oro, la primera decisión será clasificar el material básico para establecer el rango de propiedades a medir. Con tan solo tocar la superficie sabremos si es un buen o mal conductor térmico, al sentir frío o calor. Con el tiempo, la experiencia personal de tratar con diferentes materiales nos permitirá evaluar los niveles intermedios de ambos. Resulta especialmente útil para indicar la anisotropía en propiedades tales como la diferencia 7:3:1 para los ejes del cristal de galio. Sin embargo, la condición de la superficie puede influir en la respuesta y se debe considerar en una medición.
Además, es esencial brindar u obtener suficiente información detallada para identificar el material y la muestra. Probablemente esto sea algo evidente pero no siempre se lo reconoce ni se informa de manera completa y con posterioridad en las publicaciones, de modo tal que facilite la verificación y el análisis de la eficacia de cualquier valor medido. La ausencia de dichos datos respaldatorios descriptivos no ofrece una oportunidad para realizar dicho análisis ni permite una mayor evaluación que respalde el valor de medición o el desarrollo de teorías o relaciones, por ejemplo, en relación con los efectos de la temperatura o la cantidad o tamaño de un componente en particular. También resulta un factor importante en relación al punto 6, como veremos más adelante.
Esto último representa una gran decepción y un elemento de discordia para el profesor Yeram Touloukian y muchos de sus colegas del TPRC (CINDAS, en la actualidad), de la Universidad de Purdue, que han dedicado tanto esfuerzo y tiempo para recabar y evaluar los datos publicados para los materiales que figuran en el gran libro azul de varios volúmenes titulado Thermal Properties of Matter , publicado por Plenum Press, que actualmente se está digitalizando para fines generales, en particular para los técnicos analistas, como medio para comparar o justificar sus propias mediciones. Una vez determinados la forma y el rango de propiedad, la siguiente decisión es seleccionar el método adecuado.

Cualquier método para este tema consiste en la representación experimental de una ecuación basada en modelos, desarrollada para describir la distribución de la temperatura en un cuerpo semi-infinito, durante el cambio o en un punto de equilibrio posterior a la aplicación de calor. El problema principal del diseño básico de un instrumento para mediciones de estado estable es la optimización de la geometría con respecto a los tiempos de equilibrio, la disipación del calor, la transferencia de radiación y la exactitud. Los instrumentos para los métodos de flujo de calor longitudinal y radial emplean un gran sistema de muestras con configuraciones definidas más una protección adecuada para garantizar que no haya una pérdida o ganancia de calor, o que sea mínima, entre el calentador y el disipador de calor. Los resultados, en los que se puede cuantificar la pérdida de calor en caso de sospecharse, se obtienen del gradiente de temperatura medido en equilibrio y las dimensiones lineales o radiales adecuadas. Estos son todos valores medidos que permiten el desarrollo directo de una evaluación confiable sobre los niveles de exactitud y precisión. Así, todas las termocuplas deben estar fuertemente ajustadas en posición dentro o sobre la muestra para cumplir con la cuarta regla de oro.
Por el contrario, los métodos transitorios difieren por completo, ya que abordan la variación de la distribución de temperatura en el tiempo. Esto implica una ecuación del flujo de calor diferencial en donde tanto la variable de tiempo como la de espacio son importantes. Además, existen muchos modelos para estas técnicas. Cada uno posee un conjunto diferente de condiciones de contorno con una solución única que deriva en una versión adicional de un método específico. Otra característica significativa es el modo de tratamiento de la pérdida de calor, que se puede considerar insignificante, ya sea por el corto tiempo implicado o por la inclusión de un término o constante adicional en la ecuación, que se puede eliminar posteriormente a través de una medición adicional bajo diferentes condiciones experimentales. Sin embargo, estos factores ilustran que con diversas opciones de parámetros no cuantificados disponibles, se genera una fuente de incertidumbre potencial, que afecta los niveles de exactitud.
Normalmente, dichas técnicas determinan la efusividad térmica mediante la que se puede calcular la conductividad térmica, a través de los valores de densidad y calor específico. Sin embargo, bajo determinadas condiciones experimentales, se puede determinar la conductividad térmica de manera directa, pero no todos los modelos son equivalentes al considerar la precisión y la exactitud. Por ejemplo, los modelos para las técnicas de fuente de línea transitoria y fuente plana transitoria son similares y se basan en el flujo de calor simétrico uniforme desarrollado en la muestra, pero en la versión modificada de la última, el flujo de calor es asimétrico y se desarrolla en la superficie de la muestra, por lo que no sigue el modelo. En resumen, las técnicas transitorias son relativamente simples en términos de instrumento y procedimiento. Son rápidas para operar y utilizan cantidades relativamente pequeñas y formas de material homogéneo como muestra. Tal como se mencionó en el blog anterior, debido a la necesidad cada vez mayor de contar con datos sobre la propiedad térmica de materiales de todo tipo, se han vuelto populares, en especial con el método ‘universal’ disponible en el mercado.
La descripción de Fourier del flujo de calor solo aborda el modo de conducción dominante de la transferencia de calor en materiales isotrópicos. Un método de medición ofrece un valor único cuantificado de conductancia térmica solo para la muestra de prueba. Suponiendo que la muestra es densa y homogénea, y si se introduce la dimensión de longitud en la ecuación, el valor medido se convierte en conductividad térmica. Así, para todos los materiales heterogéneos y de menor densidad en donde la transferencia de calor incluye los efectos de la convección y/o la radiación, en particular a temperatura elevada, y se hace significativa, ahora se sabe que la propiedad medida es una conductividad térmica aparente o efectiva. Además, la convección se puede dar en materiales porosos de baja densidad al someterlos al uso de grandes diferencias de temperatura con un flujo de calor vertical ascendente.
Tanto la medición de la “conductividad térmica” como la interpretación del resultado medido, ahora deben incluir y permitir los efectos que indican que la propiedad solo puede visualizarse como material de muestra que depende del medioambiente. En consecuencia, estos límites más rigurosos brindan una mayor responsabilidad a quienes trabajan en la comunidad de la medición térmica, en especial, al decidir el mejor método o el más apropiado para lograr la precisión y exactitud deseadas. Durante todos mis años de experiencia activa como proveedor de información, estoy seguro de que el pedido más común que me hicieron fue simplemente “mide la conductividad térmica del material Z, a una temperatura fija determinada o sobre la temperatura X e Y”. Además, estoy seguro de que el cliente esperaba una respuesta simple, pero se sorprendió por completo al recibir muchos interrogantes sobre los factores antes mencionados. Este es un gran ejemplo que ilustra las razones de las reglas de oro 6 y 7.
Al examinar un poco más, si se sabe o se considera que el material es un sólido homogéneo relativamente “puro”, la medición solicitada puede realizarse midiendo los materiales en los primeros dos subgrupos, ya sea a través de un método de varilla longitudinal de estado estable o de placa comparativa, o mediante una técnica de fuente plana o de línea transitoria. Para el primer caso, la muestra será de forma definida y de tamaño relativamente grande. Para los métodos transitorios, en general se trata de una placa o un disco de dimensiones relativamente pequeñas. Si se debe determinar la propiedad a lo largo de un rango de temperatura, se deberán realizar las mediciones a intervalos regulares y apropiados de temperatura media para todo el rango y con una diferencia de temperatura en la muestra del orden de 10 k a 30 k para el método de estado estable.
Los niveles de exactitud de cada uno de estos métodos se indican en el rango requerido o por encima del mismo y, de ser posible, se deberán hacer todos los esfuerzos correspondientes por demostrar que los valores medidos están dentro del nivel aceptable. Esta cuestión puede abordarse a partir de consideraciones teóricas. Según la teoría básica de conducción por fonones en sólidos ‘puros’ por encima de la temperatura de Debye del material, la conductividad térmica es inversamente proporcional a la temperatura absoluta. Esto puede emplearse si se sabe cuál es la temperatura de Debye para el material de la muestra y si hay suficientes puntos de datos para ilustrar dicha relación. Desafortunadamente, no puede emplearse para una medición a una única temperatura o en sólidos heterogéneos.
Sin embargo, para los metales y las aleaciones, la confianza en los valores medidos se ilustra mejor con la ley de Wiedemann-Franz que se basa en la conducción por electrones. La misma establece que el cociente entre el aporte electrónico de la conductividad térmica y la conductividad eléctrica del metal es proporcional a la temperatura, y adquirió relevancia al demostrar que era una constante, el Número de Lorenz, L, a todas las temperaturas. La modificación mediante la inclusión de una constante para el componente del fonón (debido a impurezas, contornos de grano, etc.) propuso relaciones para numerosos sistemas de aleaciones basadas en metales, desde el aluminio hasta el circonio, que pueden utilizarse para calcular valores de conductividad térmica a un nivel del 5% para las aleaciones que no involucran cantidades significativas de carbono y silicio. La medición de la resistividad eléctrica es simple, y una medición de ambas propiedades brinda una evaluación interna de la eficacia de la medición cuando L es cercano al valor esperado, lo que justifica plenamente la regla de oro número 5.
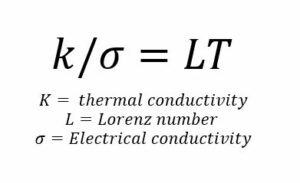
Lo que queda es un gran grupo de materiales y sistemas que incluyen todas las aislaciones térmicas y muchos tipos de sólidos porosos, celulares, fibrosos, particulados, en capas, rígidos, menos homogéneos y de baja conductividad térmica (0,01 a 10 W/m.k). Para las aislaciones térmicas, las decisiones sobre el método de medición se basaron en la experiencia obtenida mediante el uso del medidor de flujo de calor y de placa caliente que cumple con las normas ISO. Se demostró que alcanza una exactitud del 5%. El área representativa de la muestra debe ser de un diámetro mayor a 10 cm2 y 60 cm2 para las muestras de hasta 7,5 cm y 15 cm de espesor, respectivamente. Dichos requisitos eliminan o restringen fuertemente el uso de los métodos transitorios actuales debido a la pequeña superficie de la unidad de la sonda.
Sin embargo, se pueden emplear los métodos de estado estable transitorio y comparativo para los otros sólidos porosos, por lo que es importante garantizar que el tamaño de la muestra sea representativo del material.










